线段树(Segment Tree)常用于解决区间统计问题。求最值,区间和等操作均可使用该数据结构。
线段树的最简单的实现是通过数组(通过数组是为了让查找单个元素可以在O(1)的时间内做到),就像最小堆可以用数组实现一样。
比较好的资料可以参考:Segment Tree Set 1 (Sum of given range) - GeeksforGeeks
下面我们以数组[18, 17, 13, 19, 15, 11, 20, 12, 33, 25]为例。
具体构造如图所示:
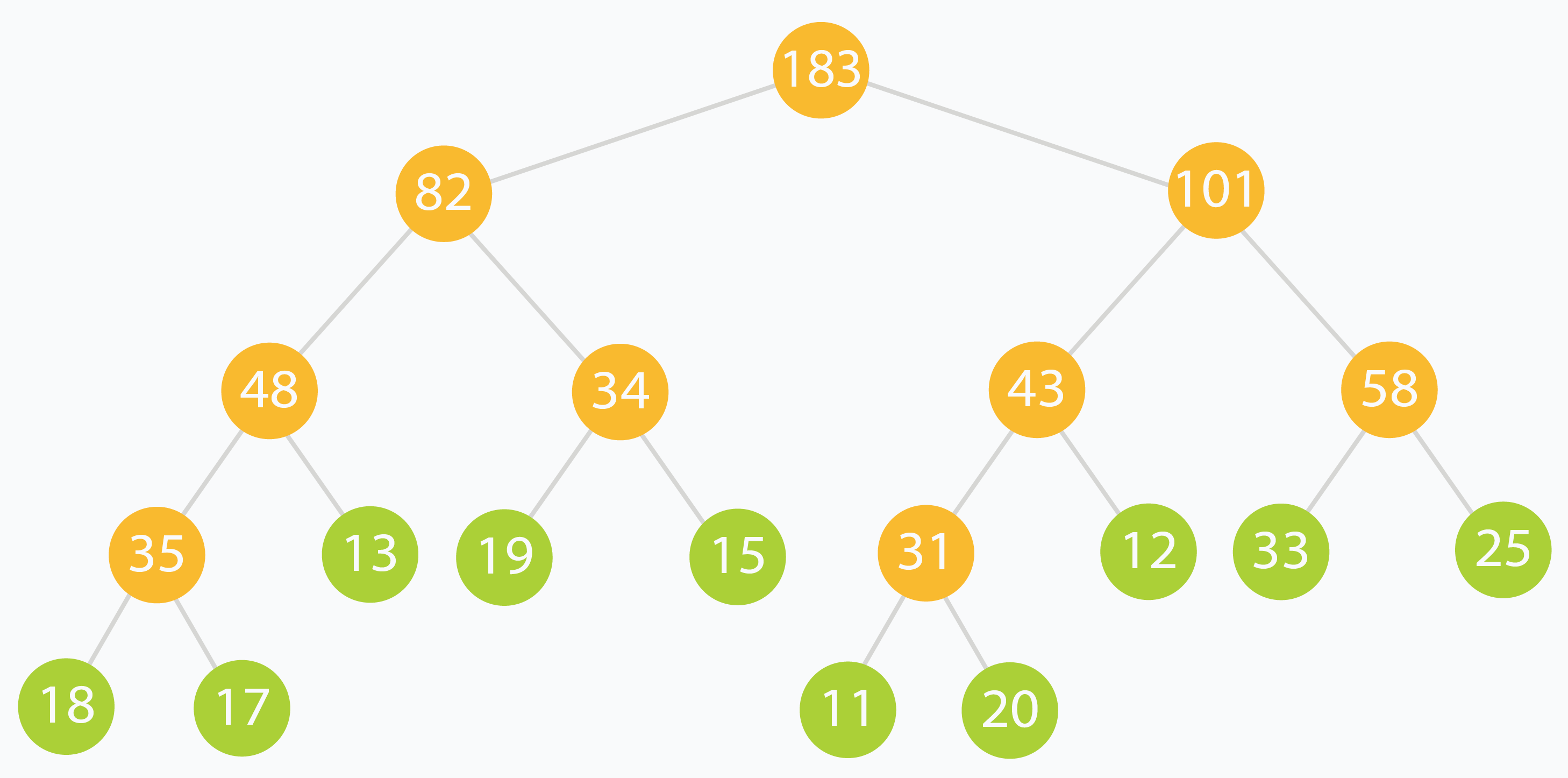
1.叶节点代表的是原始数组中的值
2.内部节点代表该节点下的叶子节点的和
3.根节点代表所有数的和
既然结构定了,那么就要决定如何构造数组,实现这个构造。
模仿最小堆,根节点放在数组的最前面,构造大小为2N的数组,原始数组的N个数放在后面。
Java代码如下:
class SegmentTree {
int[] segmentTree;
int n;
public SegmentTree(int[] nums) {
if (nums.length > 0) {
n = nums.length;
segmentTree = new int[n * 2];
//把原数组拷贝到新数组的后半部分
System.arraycopy(nums, 0, segmentTree, 0 + n, n);
//计算区域和
for (int i = n - 1; i > 0; i--) {
segmentTree[i] = segmentTree[i * 2] + segmentTree[i * 2 + 1];
}
}
}
}
以数组[18, 17, 13, 19, 15, 11, 20, 12, 33, 25]为例,建树完成后的结果为[null, 183, 125, 58, 90, 35, 32, 26, 32, 58, 18, 17, 13, 19, 15, 11, 20, 12, 33, 25]。
既然建树完成了,那么可以进行更新值和求区域和的操作。
更新值需要先更新值本身,然后再依次更新父节点:
public void update(int pos, int val) {
pos = pos + n;
//更新叶节点值
segmentTree[pos] = val;
pos /= 2;
while (pos > 0) {
//更新父节点值
segmentTree[pos] = segmentTree[pos * 2] + segmentTree[pos * 2 + 1];
pos /= 2;
}
}
求区域和的操作如下:
public int sumRange(int left, int right) {
left += n;
right += n;
int sum = 0;
while (left <= right) {
//判断左索引节点是否是父节点的右子节点
if ((left % 2) == 1) {
sum += segmentTree[left];
left++;
}
//判断右索引节点是否是父节点的左子节点
if ((right % 2) == 0) {
sum += segmentTree[right];
right--;
}
left /= 2;
right /= 2;
}
return sum;
}
求和的思路比更新值的思路更复杂,下面以如下这张图为例,数组为[2, 4, 5, 7, 8, 9],求[4, 5, 7, 8]的和
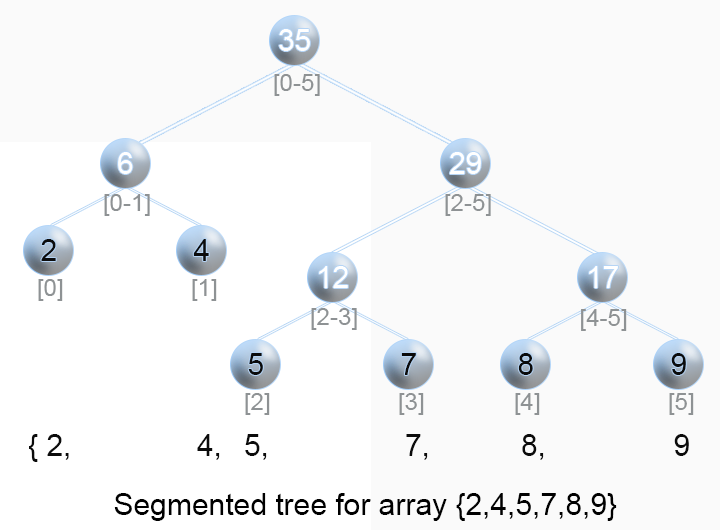
1.先建树,建树结果为[0, 35, 29, 6, 12, 17, 2, 4, 5, 7, 8, 9],索引从0到11.
2.我们要求从索引1到索引4的和,也就是树中索引从7到11的值:sum=index(7)+index(8)+index(9)+index(10)+index(11)
3.左索引7号位不能整除2,意味着是父节点的右子树,而父节点包含的左字数是不在求和范围内的,因此直接加上该索引的值,并将左索引右移一位,左索引变为8,此时结果如下:sum=4+index(8)+index(9)+index(10)+index(11)
4.左索引经过变更,此时已经成为父节点的左子树,因此左索引整除2获得父节点索引4,此时结果如下:sum=4+index(4)+index(10)+index(11)
4.右索引11不能整除2,意味着是父节点的右子树,而左子树刚好在求和范围内,无需变更索引。
5.右索引整除2获得父节点,索引变为5,此时结果如下:sum=4+index(4)+index(5)
6.左索引可以整除2,意味是父节点的左子树,无需变更索引
7.右节点不能整除2,意味着是父节点的右子树,而左子树刚好在求和范围内,无需变更索引
8.左索引除以2获得父节点索引2,而右节点除以2后与左节点相等,所以此时结果如下:sum=4+index(2)
完整代码如下:
class SegmentTree {
int[] segmentTree;
int n;
public SegmentTree(int[] nums) {
if (nums.length > 0) {
n = nums.length;
segmentTree = new int[n * 2];
//把原数组拷贝到新数组的后半部分
System.arraycopy(nums, 0, segmentTree, 0 + n, n);
//计算区域和
for (int i = n - 1; i > 0; i--) {
segmentTree[i] = segmentTree[i * 2] + segmentTree[i * 2 + 1];
}
}
}
public void update(int pos, int val) {
pos = pos + n;
//更新叶节点值
segmentTree[pos] = val;
pos /= 2;
while (pos > 0) {
//更新父节点值
segmentTree[pos] = segmentTree[pos * 2] + segmentTree[pos * 2 + 1];
pos /= 2;
}
}
public int sumRange(int left, int right) {
left += n;
right += n;
int sum = 0;
while (left <= right) {
//判断左索引节点是否是父节点的右子节点
if ((left % 2) == 1) {
sum += segmentTree[left];
left++;
}
//判断右索引节点是否是父节点的左子节点
if ((right % 2) == 0) {
sum += segmentTree[right];
right--;
}
left /= 2;
right /= 2;
}
return sum;
}
}
题目地址:Range Sum Query - Mutable - LeetCode
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]
sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:
The array is only modifiable by the update function. You may assume the number of calls to update and sumRange function is distributed evenly.
这道题目应该是很久之前看到的一道算法笔试题。
这道题目看起来不难,如果直接用暴力的做法会超时。 看到了别人有个取巧的做法:
class NumArray:
def __init__(self, nums: List[int]):
self.nums = nums
self.sum = sum(nums)
self.len = len(nums)
def update(self, i: int, val: int) -> None:
self.sum += val-self.nums[i]
self.nums[i] = val
def sumRange(self, i: int, j: int) -> int:
ran = j-i
if ran < self.len-ran:
return sum(self.nums[i:j+1])
else:
return self.sum-sum(self.nums[:i])-sum(self.nums[j+1:])
时间的耗时显著减少,可以勉强通过。
这道题目真正的做法是线段树,Segment Tree。我承认之前我没听说过这个数据结构,但在网上查找资料后发现,线段树好像也是一个经典的高级的数据结构。
Java解法如下:
class NumArray {
int[] segmentTree;
int n;
public NumArray(int[] nums) {
if (nums.length > 0) {
n = nums.length;
segmentTree = new int[n * 2];
//把原数组拷贝到新数组的后半部分
System.arraycopy(nums, 0, segmentTree, 0 + n, n);
//计算区域和
for (int i = n - 1; i > 0; i--) {
segmentTree[i] = segmentTree[i * 2] + segmentTree[i * 2 + 1];
}
}
}
public void update(int pos, int val) {
pos = pos + n;
//更新叶节点值
segmentTree[pos] = val;
pos /= 2;
while (pos > 0) {
//更新父节点值
segmentTree[pos] = segmentTree[pos * 2] + segmentTree[pos * 2 + 1];
pos /= 2;
}
}
public int sumRange(int left, int right) {
left += n;
right += n;
int sum = 0;
while (left <= right) {
//判断左索引节点是否是父节点的右子节点
if ((left % 2) == 1) {
sum += segmentTree[left];
left++;
}
//判断右索引节点是否是父节点的左子节点
if ((right % 2) == 0) {
sum += segmentTree[right];
right--;
}
left /= 2;
right /= 2;
}
return sum;
}
}
文档信息
- 本文作者:last2win
- 本文链接:https://last2win.com/2020/01/28/LeetCode-307-Range-Sum-Query-Mutable-Java/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)